
Machine Learning (ML) and Artificial Intelligence (AI) algorithms are increasingly powering our modern society and leaving their mark on everything from finance to healthcare, to transportation. If the late half of the 20th century was about the general progress in computing and connectivity (internet infrastructure), the 21st century is shaping up to be dominated by intelligent computing and a race toward smarter machines.
Most of the discussion and awareness about these novel computing paradigms, however, circle around the so-called ‘supervised learning’, in which Deep Learning (DL) occupies a central position. The recent advancement and astounding success of Deep Neural Networks (DNN) - from disease classification to image segmentation to speech recognition - has led to much excitement and application of DNNs in all facets of high-tech systems.
DNN systems, however, need a lot of training data (labeled samples for which the answer is already known) to work properly and they do not exactly mimic the way human beings learn and apply their intelligence. Almost all AI experts agree that simply scaling up the size and speed of DNN-based systems will never lead to true "human-like" AI systems or anything even close to it.
Consequently, there is a lot of research and interest in exploring ML/AI paradigms and algorithms that go beyond the realm of supervised learning, and try to follow the curve of the human learning process. Reinforcement Learning (RL) is the most widely researched and exciting of these.
In this article, we briefly discuss how, modern DL and RL, can be enmeshed together in a field called Deep Reinforcement Learning (DRL) to produce powerful AI systems.
What is Deep Reinforcement Learning?
Humans excel at solving a wide variety of challenging problems, from low-level motor control (e.g. walking, running, playing tennis) to high-level cognitive tasks (e.g. doing mathematics, writing poetry, conversation).
Reinforcement learning aims to enable a software/hardware agent to mimic this human behavior through well-defined, well-designed computing algorithms. The goal of such a learning paradigm is not to map labeled examples in a simple input/output functional manner (like a standalone DL system) but to build a strategy which helps the intelligent agent to take action in a sequence with the goal of fulfilling some ultimate goal.
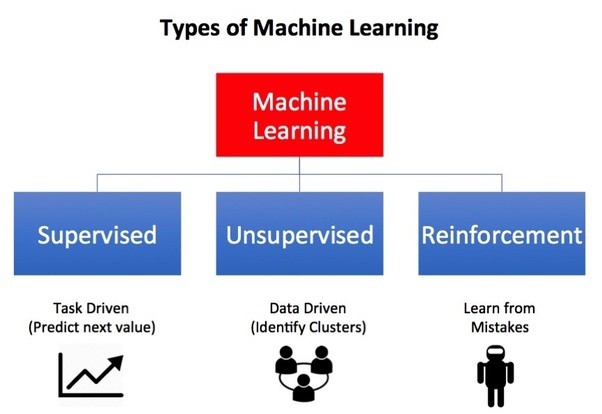
Figure source: “What are the types of machine learning”
More formally, RL refers to goal-oriented algorithms, which learn how to attain a complex objective (goal) or how to maximize along a particular dimension over many steps. The following examples illustrate their use:
- A board game which maximizes the probability of winning
- A financial simulation maximizing the gain of a transaction
- A robot moving through a complex environment minimizing the error in its movements
The idea is that the agent receives input from the environment through sensor data, processes it using RL algorithms, and then takes an action towards satisfying the predetermined goal. This is very similar to how we humans behave in our daily life.
Some Essential Definitions in Deep Reinforcement Learning
It is useful, for the forthcoming discussion, to have a better understanding of some key terms used in RL.
Agent: A software/hardware mechanism which takes certain action depending on its interaction with the surrounding environment; for example, a drone making a delivery, or Super Mario navigating a video game. The algorithm is the agent.
Action: An action is one of all the possible moves the agent can make. Action is almost self-explanatory, but it should be noted that agents usually choose from a list of discrete, possible actions.
Environment: The world through which the agent moves, and which responds to the agent. The environment takes the agent's current state and action as input, and returns as output the agent's reward and its next state.
State: A state is a concrete and immediate situation in which the agent finds itself; i.e. a specific place and moment, an instantaneous configuration that puts the agent in relation to other significant things. An example is a particular configuration of a chessboard.
Reward: A reward is feedback by which we measure the success or failure of an agent's actions in a given state. For example, in a game of chess, important actions such as eliminating the bishop of the opponent can bring some reward, while winning the game may bring a big reward. Negative rewards are also defined in a similar sense, e.g. loss in a game.
Discount factor: The discount factor is a multiplier. Future rewards, as discovered by the agent, are multiplied by this factor in order to dampen these rewards' cumulative effect on the agent's current choice of action. This is at the heart of RL, i.e. gradually reducing the value of future rewards so that recent actions are given more weight. This is critically important for a paradigm that works on the principle of 'delayed action'.
Policy: The policy is the strategy that the agency employs to determine the next action based on the current state. It maps states to actions, the actions that promise the highest reward.
Value: The expected long-term return with the discount, as opposed to the short-term reward. The value is defined as the expected long-term return of the current state under a particular policy.
Q-value or action-value: Q-value is similar to value, except that it takes an extra parameter, the current action. It refers to the long-term return of an action taking a specific action under a specific policy from the current state.
Common Mathematical and Algorithmic Frameworks
Some of the common mathematical frameworks to solve RL problems are as follows:
Markov Decision Process (MDP): Almost all the RL problems can be framed as MDPs. All states in MDP have the "Markov" property, referring to the fact that the future only depends on the current state, not the history of the states.
Bellman Equations: Bellman equations refer to a set of equations that decompose the value function into the immediate reward plus the discounted future values.
Dynamic Programming: When the model of the system (agent + environment) is fully known, following Bellman equations, we can use Dynamic Programming (DP) to iteratively evaluate value functions and improve policy.
Value iteration: It is an algorithm that computes the optimal state value function by iteratively improving the estimate of the value. The algorithm initializes the value function to arbitrary random values and then repeatedly updates the Q-value and value function values until they converge.
Policy iteration: Since the agent only cares about finding the optimal policy, sometimes the optimal policy will converge before the value function. Therefore, policy-iteration, instead of repeatedly improving the value-function estimate, re-defines the policy at each step and computes the value according to this new policy until the policy converges.
Q-learning: This is an example of a model-free learning algorithm. It does not assume that the agent knows anything about the state-transition and reward models. However, the agent will discover what are the good and bad actions by trial and error. The basic idea of Q-Learning is to approximate the state-action pairs Q-function from the samples of Q-value function that we observe during the agent's interactions with the environment. This approach is known as Time-Difference Learning.
Figure: An example RL problem solved by Q-learning (trial-and-error-observation). The dynamics and model of the environment, i.e. the whole physics of the movement, is not known.
The challenge of Model-Free RL
Q-learning is a simple yet powerful method for solving RL problems and, in theory, can scale up for large problems without introducing additional mathematical complexity. The basic Q-learning can be done with the help of a recursive equation,
Here,
Q(s,a): Q-value function,
s: State
s’, s’’: Future states
a: Action
γ: Discount factor
For small problems, one can start by making arbitrary assumptions for all Q-values. With trial-and-error, the Q-table gets updated and the policy progresses towards a convergence. The updating and choosing action is done randomly and, as a result, the optimal policy may not represent a global optimum, but it works for all practical purposes.
However, constructing and storing a set of Q-tables for a large problem quickly becomes a computational challenge as the problem size grows. For example, in games like chess or Go, the number of possible states (sequence of moves) grows exponentially with the number of steps one wants to calculate ahead. Therefore,
- the amount of memory required to save and update that table would increase as the number of states increases
- the amount of time required to explore each state to create the required Q-table would be unrealistic
Techniques such as Deep-Q learning try to tackle this challenge using ML.
Deep-Q-learning
As the name suggests, Deep Q-learning, instead of maintaining a large Q-value table, utilizes a neural network to approximate the Q-value function from the given input of action and state. In some formulations, the state is given as the input and the Q-value of all possible actions is generated as the output. The neural network is called Deep-Q-Network (DQN). The basic idea is shown below,
But working with a DQN can be quite challenging. In traditional DL algorithms, we randomize the input samples so the input class is quite balanced and somewhat stable across various training batches. In RL, the search gets better as the exploration phase progresses. This changes the input and action spaces constantly. In addition, as the knowledge about the environment gets better, the target value of Q is automatically updated. In short, both the input and output are under frequent changes for a straightforward DQN system.
To solve this, DQN introduces the concepts of experience replay and target network to slow down the changes so that the Q-table can be learned gradually and in a controlled/stable manner.
Experience replay stores a certain amount of state-action-reward values (e.g. last one million) in a specialized buffer. Training of the Q-function is done with mini-batches of random samples from this buffer. Therefore, the training samples are randomized and behave closer to a typical case of supervised learning in traditional DL. This is akin to having a highly-efficient short-term memory, which can be relied upon while exploring the unknown environment.
In addition, DQN generally employs two networks for storing the values of Q. One is constantly updated while the second one, the target network, is synchronized from the first network at regular intervals. The target network is used to retrieve the Q value such that the changes for the target value are less volatile.
Examples of Deep Reinforcement Learning (DRL)
Playing Atari Games (DeepMind)
DeepMind, a London based startup (founded in 2010), which was acquired by Google/Alphabet in 2014, made a pioneering contribution to the field of DRL when it successfully used a combination of convolutional neural network (CNN) and Q-learning to train an agent to play Atari games from just raw pixel input (as sensory signals). The details can be found here.
Playing Atari with Deep Reinforcement Learning
Alpha Go and Alpha Go Zero (DeepMind)
The game of Go originated in China over 3,000 years ago and it is known as the most challenging classical game for AI because of its complexity. Standard AI methods, which test all possible moves and positions using a search tree, can't handle the sheer number of possible Go moves or evaluate the strength of each possible board position.
Using DRL techniques and a novel search algorithm, DeepMind developed AlphaGo, which is the first computer program to defeat a professional human Go player, the first to defeat a Go world champion, and is arguably the strongest Go player in history.
A better version of this Alpha Go is called Alpha Go Zero. Here, the system is initiated with a neural network that has zero knowledge about the game of Go or the rules. It then plays games against itself, by combining this neural network with a powerful search algorithm. During repeated gameplay, the neural network is tuned and updated to predict moves, as well as the eventual winner of the games. This updated neural network is then recombined with the search algorithm to create a new, stronger version of AlphaGo Zero, and the process begins again. In each iteration, the performance of the system improves by a small amount and the quality of the self-play games increases.
Uses in the Oil & Gas Industry
Royal Dutch Shell has been deploying reinforcement learning in its exploration and drilling endeavors to bring the high cost of gas extraction down, as well as improve multiple steps in the whole supply chain. DL algorithms, trained on the historical drilling data, as well as advanced physics-based simulations, are used to steer the gas drills as they move through a subsurface. The DRL technology also utilizes mechanical data from the drill bit - pressure and bit temperature - as well as subsurface-dependent seismic survey data. Read more here:
The Incredible Ways Shell Uses Artificial Intelligence To Help Transform The Oil And Gas Giant.
Autonomous Driving
While still not mainstream, tremendous potential exists for DRL to be applied in various challenging problem domains for autonomous vehicles.
- Vehicle control
- Ramp merging
- Perception of individual driving style
- Multiple-goal RL for overtaking safely
This paper explains the concepts clearly: Exploring applications of deep reinforcement learning for real-world autonomous driving systems.
Main Takeaways from What You Need to Know About Deep Reinforcement Learning
Reinforcement learning is the most promising candidate for truly-scalable, human-compatible, AI systems, and for the ultimate progress towards Artificial General Intelligence (AGI). However, for almost all practical problems, the traditional RL algorithms are extremely hard to scale and apply due to exploding computational complexity.
Deep learning, which has transformed the field of AI in recent years, can be applied to the domain of RL in a systematic and efficient manner to partially solve this challenge. This approach has given rise to intelligent agents like AlphaGo, which can learn the rules of a game (and therefore, by generalization, rules about the external world) entirely from scratch, without explicit training and rule-based programming.
The future and promise of DRL are therefore bright and shiny. In this article, we touched upon the basics of RL and DRL to give the readers a flavor of this powerful sub-field of AI.

What You Need to Know About Deep Reinforcement Learning
Machine Learning (ML) and Artificial Intelligence (AI) algorithms are increasingly powering our modern society and leaving their mark on everything from finance to healthcare, to transportation. If the late half of the 20th century was about the general progress in computing and connectivity (internet infrastructure), the 21st century is shaping up to be dominated by intelligent computing and a race toward smarter machines.
Most of the discussion and awareness about these novel computing paradigms, however, circle around the so-called ‘supervised learning’, in which Deep Learning (DL) occupies a central position. The recent advancement and astounding success of Deep Neural Networks (DNN) - from disease classification to image segmentation to speech recognition - has led to much excitement and application of DNNs in all facets of high-tech systems.
DNN systems, however, need a lot of training data (labeled samples for which the answer is already known) to work properly and they do not exactly mimic the way human beings learn and apply their intelligence. Almost all AI experts agree that simply scaling up the size and speed of DNN-based systems will never lead to true "human-like" AI systems or anything even close to it.
Consequently, there is a lot of research and interest in exploring ML/AI paradigms and algorithms that go beyond the realm of supervised learning, and try to follow the curve of the human learning process. Reinforcement Learning (RL) is the most widely researched and exciting of these.
In this article, we briefly discuss how, modern DL and RL, can be enmeshed together in a field called Deep Reinforcement Learning (DRL) to produce powerful AI systems.
What is Deep Reinforcement Learning?
Humans excel at solving a wide variety of challenging problems, from low-level motor control (e.g. walking, running, playing tennis) to high-level cognitive tasks (e.g. doing mathematics, writing poetry, conversation).
Reinforcement learning aims to enable a software/hardware agent to mimic this human behavior through well-defined, well-designed computing algorithms. The goal of such a learning paradigm is not to map labeled examples in a simple input/output functional manner (like a standalone DL system) but to build a strategy which helps the intelligent agent to take action in a sequence with the goal of fulfilling some ultimate goal.

Figure source: “What are the types of machine learning”
More formally, RL refers to goal-oriented algorithms, which learn how to attain a complex objective (goal) or how to maximize along a particular dimension over many steps. The following examples illustrate their use:
- A board game which maximizes the probability of winning
- A financial simulation maximizing the gain of a transaction
- A robot moving through a complex environment minimizing the error in its movements
The idea is that the agent receives input from the environment through sensor data, processes it using RL algorithms, and then takes an action towards satisfying the predetermined goal. This is very similar to how we humans behave in our daily life.
Some Essential Definitions in Deep Reinforcement Learning
It is useful, for the forthcoming discussion, to have a better understanding of some key terms used in RL.
Agent: A software/hardware mechanism which takes certain action depending on its interaction with the surrounding environment; for example, a drone making a delivery, or Super Mario navigating a video game. The algorithm is the agent.
Action: An action is one of all the possible moves the agent can make. Action is almost self-explanatory, but it should be noted that agents usually choose from a list of discrete, possible actions.
Environment: The world through which the agent moves, and which responds to the agent. The environment takes the agent's current state and action as input, and returns as output the agent's reward and its next state.
State: A state is a concrete and immediate situation in which the agent finds itself; i.e. a specific place and moment, an instantaneous configuration that puts the agent in relation to other significant things. An example is a particular configuration of a chessboard.
Reward: A reward is feedback by which we measure the success or failure of an agent's actions in a given state. For example, in a game of chess, important actions such as eliminating the bishop of the opponent can bring some reward, while winning the game may bring a big reward. Negative rewards are also defined in a similar sense, e.g. loss in a game.
Discount factor: The discount factor is a multiplier. Future rewards, as discovered by the agent, are multiplied by this factor in order to dampen these rewards' cumulative effect on the agent's current choice of action. This is at the heart of RL, i.e. gradually reducing the value of future rewards so that recent actions are given more weight. This is critically important for a paradigm that works on the principle of 'delayed action'.
Policy: The policy is the strategy that the agency employs to determine the next action based on the current state. It maps states to actions, the actions that promise the highest reward.
Value: The expected long-term return with the discount, as opposed to the short-term reward. The value is defined as the expected long-term return of the current state under a particular policy.
Q-value or action-value: Q-value is similar to value, except that it takes an extra parameter, the current action. It refers to the long-term return of an action taking a specific action under a specific policy from the current state.
Common Mathematical and Algorithmic Frameworks
Some of the common mathematical frameworks to solve RL problems are as follows:
Markov Decision Process (MDP): Almost all the RL problems can be framed as MDPs. All states in MDP have the "Markov" property, referring to the fact that the future only depends on the current state, not the history of the states.
Bellman Equations: Bellman equations refer to a set of equations that decompose the value function into the immediate reward plus the discounted future values.
Dynamic Programming: When the model of the system (agent + environment) is fully known, following Bellman equations, we can use Dynamic Programming (DP) to iteratively evaluate value functions and improve policy.
Value iteration: It is an algorithm that computes the optimal state value function by iteratively improving the estimate of the value. The algorithm initializes the value function to arbitrary random values and then repeatedly updates the Q-value and value function values until they converge.
Policy iteration: Since the agent only cares about finding the optimal policy, sometimes the optimal policy will converge before the value function. Therefore, policy-iteration, instead of repeatedly improving the value-function estimate, re-defines the policy at each step and computes the value according to this new policy until the policy converges.
Q-learning: This is an example of a model-free learning algorithm. It does not assume that the agent knows anything about the state-transition and reward models. However, the agent will discover what are the good and bad actions by trial and error. The basic idea of Q-Learning is to approximate the state-action pairs Q-function from the samples of Q-value function that we observe during the agent's interactions with the environment. This approach is known as Time-Difference Learning.
Figure: An example RL problem solved by Q-learning (trial-and-error-observation). The dynamics and model of the environment, i.e. the whole physics of the movement, is not known.
The challenge of Model-Free RL
Q-learning is a simple yet powerful method for solving RL problems and, in theory, can scale up for large problems without introducing additional mathematical complexity. The basic Q-learning can be done with the help of a recursive equation,
Here,
Q(s,a): Q-value function,
s: State
s’, s’’: Future states
a: Action
γ: Discount factor
For small problems, one can start by making arbitrary assumptions for all Q-values. With trial-and-error, the Q-table gets updated and the policy progresses towards a convergence. The updating and choosing action is done randomly and, as a result, the optimal policy may not represent a global optimum, but it works for all practical purposes.
However, constructing and storing a set of Q-tables for a large problem quickly becomes a computational challenge as the problem size grows. For example, in games like chess or Go, the number of possible states (sequence of moves) grows exponentially with the number of steps one wants to calculate ahead. Therefore,
- the amount of memory required to save and update that table would increase as the number of states increases
- the amount of time required to explore each state to create the required Q-table would be unrealistic
Techniques such as Deep-Q learning try to tackle this challenge using ML.
Deep-Q-learning
As the name suggests, Deep Q-learning, instead of maintaining a large Q-value table, utilizes a neural network to approximate the Q-value function from the given input of action and state. In some formulations, the state is given as the input and the Q-value of all possible actions is generated as the output. The neural network is called Deep-Q-Network (DQN). The basic idea is shown below,
But working with a DQN can be quite challenging. In traditional DL algorithms, we randomize the input samples so the input class is quite balanced and somewhat stable across various training batches. In RL, the search gets better as the exploration phase progresses. This changes the input and action spaces constantly. In addition, as the knowledge about the environment gets better, the target value of Q is automatically updated. In short, both the input and output are under frequent changes for a straightforward DQN system.
To solve this, DQN introduces the concepts of experience replay and target network to slow down the changes so that the Q-table can be learned gradually and in a controlled/stable manner.
Experience replay stores a certain amount of state-action-reward values (e.g. last one million) in a specialized buffer. Training of the Q-function is done with mini-batches of random samples from this buffer. Therefore, the training samples are randomized and behave closer to a typical case of supervised learning in traditional DL. This is akin to having a highly-efficient short-term memory, which can be relied upon while exploring the unknown environment.
In addition, DQN generally employs two networks for storing the values of Q. One is constantly updated while the second one, the target network, is synchronized from the first network at regular intervals. The target network is used to retrieve the Q value such that the changes for the target value are less volatile.
Examples of Deep Reinforcement Learning (DRL)
Playing Atari Games (DeepMind)
DeepMind, a London based startup (founded in 2010), which was acquired by Google/Alphabet in 2014, made a pioneering contribution to the field of DRL when it successfully used a combination of convolutional neural network (CNN) and Q-learning to train an agent to play Atari games from just raw pixel input (as sensory signals). The details can be found here.
Playing Atari with Deep Reinforcement Learning
Alpha Go and Alpha Go Zero (DeepMind)
The game of Go originated in China over 3,000 years ago and it is known as the most challenging classical game for AI because of its complexity. Standard AI methods, which test all possible moves and positions using a search tree, can't handle the sheer number of possible Go moves or evaluate the strength of each possible board position.
Using DRL techniques and a novel search algorithm, DeepMind developed AlphaGo, which is the first computer program to defeat a professional human Go player, the first to defeat a Go world champion, and is arguably the strongest Go player in history.
A better version of this Alpha Go is called Alpha Go Zero. Here, the system is initiated with a neural network that has zero knowledge about the game of Go or the rules. It then plays games against itself, by combining this neural network with a powerful search algorithm. During repeated gameplay, the neural network is tuned and updated to predict moves, as well as the eventual winner of the games. This updated neural network is then recombined with the search algorithm to create a new, stronger version of AlphaGo Zero, and the process begins again. In each iteration, the performance of the system improves by a small amount and the quality of the self-play games increases.
Uses in the Oil & Gas Industry
Royal Dutch Shell has been deploying reinforcement learning in its exploration and drilling endeavors to bring the high cost of gas extraction down, as well as improve multiple steps in the whole supply chain. DL algorithms, trained on the historical drilling data, as well as advanced physics-based simulations, are used to steer the gas drills as they move through a subsurface. The DRL technology also utilizes mechanical data from the drill bit - pressure and bit temperature - as well as subsurface-dependent seismic survey data. Read more here:
The Incredible Ways Shell Uses Artificial Intelligence To Help Transform The Oil And Gas Giant.
Autonomous Driving
While still not mainstream, tremendous potential exists for DRL to be applied in various challenging problem domains for autonomous vehicles.
- Vehicle control
- Ramp merging
- Perception of individual driving style
- Multiple-goal RL for overtaking safely
This paper explains the concepts clearly: Exploring applications of deep reinforcement learning for real-world autonomous driving systems.
Main Takeaways from What You Need to Know About Deep Reinforcement Learning
Reinforcement learning is the most promising candidate for truly-scalable, human-compatible, AI systems, and for the ultimate progress towards Artificial General Intelligence (AGI). However, for almost all practical problems, the traditional RL algorithms are extremely hard to scale and apply due to exploding computational complexity.
Deep learning, which has transformed the field of AI in recent years, can be applied to the domain of RL in a systematic and efficient manner to partially solve this challenge. This approach has given rise to intelligent agents like AlphaGo, which can learn the rules of a game (and therefore, by generalization, rules about the external world) entirely from scratch, without explicit training and rule-based programming.
The future and promise of DRL are therefore bright and shiny. In this article, we touched upon the basics of RL and DRL to give the readers a flavor of this powerful sub-field of AI.




